今天,小编给大家分享一份原创居家物理实验,这个实验的特点在于,竟然只需要手机、被子、和床就可以完成(所以这个实验约等于我每天的咸鱼生活了),是不是很神奇呢!一起来看一下吧:
预备阶段
- 材料
- 内置三轴陀螺仪的手机(也就是几乎所有手机)
- 应用市场搜索下载PhyPhox
- 床、被子,用来给跌落的手机减震
- 目标
- 验证刚体转动欧拉方程,并测量主轴惯量
如图,以符合安卓系统习惯的方式在手机上建立参考系:

由于手机自身的对称性,我们不妨假设手机的三个惯量主轴恰好沿$x, y, z$方向,相应主轴转动惯量分别为$I_1, I_2, I_3$,目测发现$I_3 > I_1 > I_2$。
手机抛出后有喜闻乐见的欧拉方程:
\[\begin{aligned} I_{1}{\dot {\omega }}_1+(I_{3}-I_{2})\omega _{2}\omega _{3}&=0\\ I_{2}{\dot {\omega }}_2+(I_{1}-I_{3})\omega _{3}\omega _{1}&=0\\ I_{3}{\dot {\omega }}_3+(I_{2}-I_{1})\omega _{1}\omega _{2}&=0 \end{aligned}\]假设牛顿力学成立,空气阻力忽略,可以有四个理论预言:
-
从运动学方程看出
\[\frac{\dot{\omega_1}}{\omega_2\omega_3},\quad \frac{\dot{\omega_2}}{\omega_1\omega_3}, \quad \frac{\dot{\omega_3}}{\omega_1\omega_2}\]三个无量纲量均应不随时间变化,将上面三个量分别记为$\eta_1, \eta_2, \eta_3$
-
记 \(\frac{I_2}{I_1} = \alpha, \quad \frac{I_3}{I_1} = \beta\)。 则应该有:
\[\alpha - \beta = \eta_1, \quad \frac{\beta - 1}{\alpha} = \eta_2, \quad \frac{1-\alpha}{\beta} = \eta_3\] -
从三个主轴转动惯量间相对大小看出 \(\alpha < 1, \quad \beta > 1\)
更进一步,如果手机密度均匀,且长宽高大致为:
\[L_x = 7.8\text{cm}, L_y = 16.4 \text{cm}, L_z = 0.7\text{cm}\]则可以由此估计出
\[\alpha \approx \text{0.23}, \quad \beta \approx \text{1.22}\]
实验部分
启动PhyPhox,按下角速度记录按钮,朝着被子扔手机,导出数据,重复多次。
结论
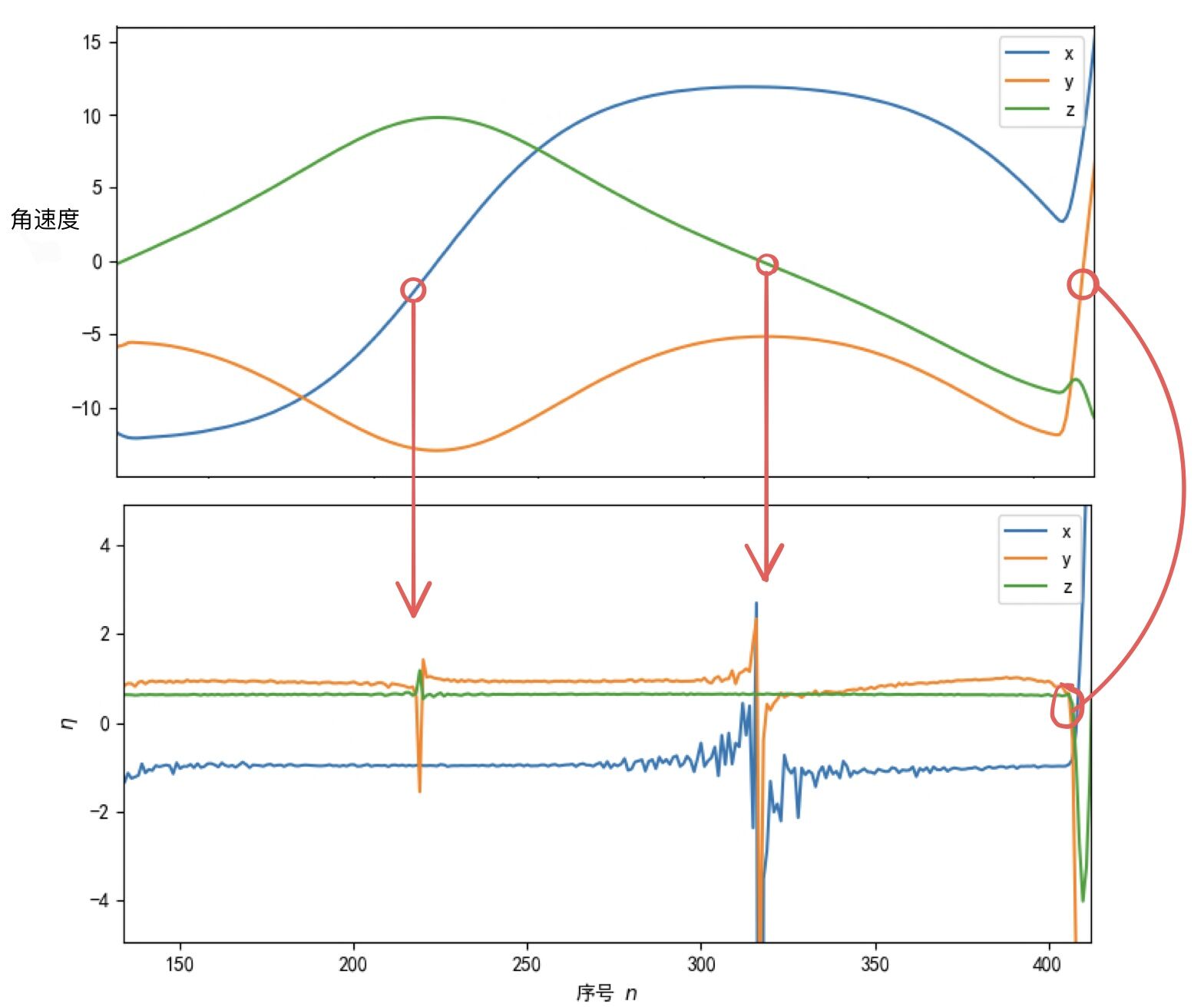
如上图,全局来看,$\eta$数值并不一直保持常数,而是会出现几个短暂的奇异点,这个也很好理解,因为$\eta$的定义中使用了除法,如果$\omega_x$降到0,$\eta_y$与$\eta_z$的相对误差都会突破天际,图线上表示为“尖峰”(见图中红色箭头)。值得庆幸的是,在两个相邻尖峰之间,我们的$\eta$基本是个常数。
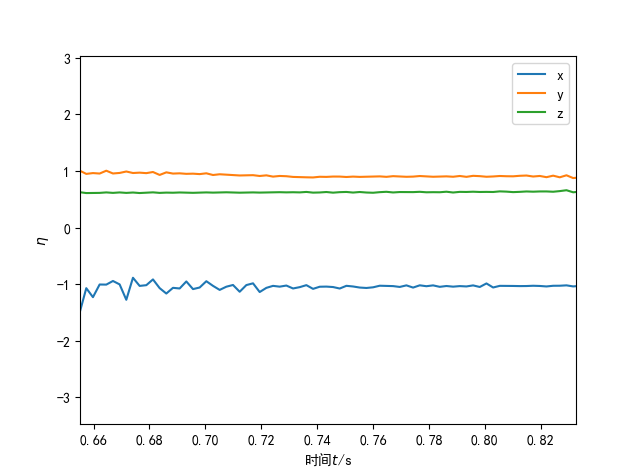
选像上图这样$\eta$近似为常数的区间,取平均,得到$\eta_i$测量值,再多次实验分析下误差,得到:
\[\eta_1 = -0.98 \pm 0.03,\quad \eta_2 = 0.92 \pm 0.01,\quad \eta_3 = 0.632 \pm 0.005\]从三个$\eta_i$可以反解出$\alpha, \beta$。三个方程两个未知数,这要求三个方程自冾。先从理论预言第二部分的后两个等式反解出$\alpha, \beta$
\[\alpha = \frac{1- \eta_3}{1+\eta_2 \eta_3}, \quad \beta = \frac{1 + \eta_2}{1 + \eta_2 \eta_3}\]得
\[\alpha = 0.233 \pm 0.003, \quad \beta = 1.21 \pm 0.01\]经过简单验算,在误差范围内确实是自冾的。于是,三个主轴转动惯量(的相对值)就算出来啦,和密度均匀时的估计结果比较一下,发现效果真的不错,相对误差竟然跌破1%!没有什么卵用但是很成功的实验又增加了!
附录
- 进一步的实验,可以将手机绑在大石头上,利用梯度下降找极值的方法,把$\eta_i$优化到最平稳,算出大石头的主轴方向相对于手机陀螺仪坐标架的转角(要用三个欧拉角描述转动,写起程序来还挺繁的。我试了一下把手机绑iPad上,能做出结果,但是数据质量很差的丫子)。
- 实在是没想出什么能在家方便地测出主轴惯量绝对值的方法QAQ,所以还是只能测他们的比值。
如果老哥老姐们有更好的办法,别忘了在评论区提醒小编喔(ノ*・ω・)ノ
