如何实现一个像那么回事儿的量子霸权实验——玻色采样

追寻通用量子计算的过程道阻且长，需要定一些短期的小目标来给大伙儿点动力，Quantum Supremacy 就是其中最小的一个目标，想法是：寻找一个量子体系，经过演化之后测量其结果。将这个过程放在经典计算机上来模拟，如果目前的超算很久才能算出来，就算是“霸权”了。近些年比较火的此类实验有潘建伟领导课题组在线性光学体系中做的玻色采样，以及Google在他们的Sycamore超导量子电路上实现的随机电路采样（quantum circuit sampling）。本篇简记一下该如何实现一个玻色采样实验。

Boson Sampling

玻色采样的问题在2011年由Aaronson et al首次提出¹，考察的原始问题是n个无相互作用不可分辨的玻色子，放进单粒子Hilbert Space维度为m的空间里，制备一个确定的初始态。初始态经过某个演化到达末态，于是如果对末态进行测量（采样）会得到一个随机分布。玻色采样就是这么一个生成符合上述要求的随机序列的问题。

m维Hilbert Space里的演化只能是一个m维酉矩阵，记成$U$，这个单粒子态的演化算符自然会诱导出一个Fock Space的n粒子子空间上的演化算符，不妨也写成$U$，这一套装置目前最适合用沿不同“路径”（如自由空间中或者波导中）传播的单光子态来实现，因为光子是人类最熟悉的玻色子，且只有在极特殊的条件下才参与相互作用。忽略偏振自由度，m条路径的入口即为m个单粒子初始态，路径间互相隧穿（耦合）就可以构造出想要的酉矩阵，出口处再分别接上单光子探测器来实现对末态的测量。如果写进占据数表象：

\[\ket{s_1 s_2 \cdots s_m}\]

表示在第1个入口送入$s_1$个光子，以此类推，$\sum_i s_i \equiv n$

如果出口处的m个探测器同时分别探测到了$t_1, t_2, \cdots$个光子，就可以认为末态是

\[\ket{t_1 t_2 \cdots t_m}\]

一个$m=4$的波色采样装置可能长成下面这个样子：

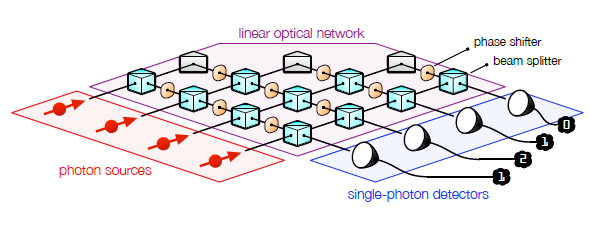
理论上讲，求目标的采样分布相当于计算下面这个式子：

\[\bra{t_1 t_2 \cdots t_m} U \ket{s_1 s_2 \cdots s_m} = \frac{\text{per} (U_{ST})}{\sqrt{\prod_i t_i ! \prod_i s_i !}}\]

里面涉及到一个n-by-n矩阵的permanent（积和式，即规范对称n重线性函数），目前对一般矩阵，计算积和式最好算法的复杂度是$O(n \cdot 2^n)$，18年在天河二号进行的并行计算²结果是，对一个50*50的矩阵算一个这样的permanent需要100分钟。

实现量子霸权要多少个光子？

简化起见，只讨论$s_i \leq 1$的情况，因为若两个光子处在同一个初态，permanent会更好算。

要用经典计算机实现随机采样，首先想到的naive算法是：n个光子（小球）放进m个单粒子态（盒子）有$C_{m+n-1}^{n}$种放法，对每种可能的末态算一遍permanent，得到概率分布之后，每次随机采样就只需要常数复杂度了。这种方法的时间复杂度为$O(C_{m+n-1}^{n} n \cdot 2^n)$

容易发现，量子光路每“成功运行”一次，获得的是一个采样结果，而上面这个naive算法求出了所有可能情况的概率，于是这两台机器严格来说解决的并不是同一个问题。我们期待能找一个经典的随机过程，让它每次生成一个服从前述分布的样本。

两位Clifford找到了这么一个算法³，将单次采样的复杂度降到了$O(n 2^n)$，（注意在量子体系里的“计算”用时其实只是光子从产生到被探测器探测到这一点儿路程的耗时）。这个算法的基本想法其实还算简单，他们首先将波色采样理解为生成一个$(r_1, r_2, \cdots, r_n)$的有序随机序列，其中每个$r_i$代表第$i$个光子在第$r_i$个出口被探测到，采样结果即是一个形如$p(r_1, r_2, \cdots, r_n)$的概率分布，我们试图构造某种循环过程，能够将$r_1$到$r_n$依次取出，构造的思路也非常暴力，根据条件概率：

\[p(r_1, r_2, \cdots, r_n) = p(r_1) p(r_2|r_1) \cdots p(r_n|r_1, r_2, \cdots r_{n-1})\]

他们理论推导出了上面条件概率的每一项，发现其中重复计算了很多相近矩阵的permanent，通过permanent的Laplace按行展开方式可以避免冗余计算，仔细化简后得到了$O(n 2^n)$的单次采样算法。经过进一步分析，他们认为50个光子是目前实现量子霸权的必要条件。

具体实现

潘建伟团队19年⁴做了n=20, m=60的实验，是迄今的规模之最，装置实物图如下：

简单来说，他们将单光子源产生的光子以20个为一组送进60*60的线性光学网络里（网络本质上依然由前面示意图里的beam-splitter, 反射镜等光学元件构成，团队找到了一种巧妙的方式将他们塞进由多层结构构成的几厘米见方的器件中（图中央的那个）。

实际实现中需要考虑的一些比较重要的问题有：

• 必须保证$U$矩阵每一个矩阵元稳定（重复实验的需要），并且要求这个矩阵足够“任意”，因为对于某些比较特殊的矩阵，经典算法总是能快速计算的，所以实验用到的那个$U$必须是“从全体U(m)矩阵中随机取一个”，我们知道，要定义随机必须先定义一个测度，幸运的是，$U(m)$作为一个性质非常好的拓扑群（locally compact Hausdorff topological group），Haar证明了，如果要求测度在群元变换操作下不变（比如U(2)中每一个元素可以看成一个spin-1/2空间上的“旋转”，空间中某个点集的“体积”显然不应该随整体的旋转而变化），那么对这样的拓扑空间赋予测度的方式是唯一的（Haar measure），于是这个矩阵每个群元应当服从的随机分布可以严格计算⁵，从而能和实验进行比较。
• 入射的光子并不全能活着到达探测器，一些会半路丢掉，他们的实验中入射20个光子最多只接收到了14个，这需要对光子丢失的机制有一些认识，并且如果光子丢的太多也就无法实现量子霸权了。
• 光子越多，出射的状态空间越大，同样的时间内某个给定出射态被探测到的次数就越少（sampling rate越低），如果每种情况一天只能见到几次，当然无法通过概率分布来和理论比较了，需要用别的方式来检查自己的实验有没有做对，比如一些类似贝叶斯分析的方法。

（未完待续(ˇωˇ」∠)_